پیش نوشت یک: دوست داشتم بیام یه چیزی همین‌طوری الکی توی روزنوشته بنویسم که به روز بشه. فشار کار هم خسته‌ام کرده بود و مغزم کار نمی‌کرد. بنابراین، مطلب تحلیلی نمی‌شد بنویسم. گفتم یه چیزی بنویسم که خیلی به مغزم فشار نیاره و بیشتر از جنس ریاضی و مبانی اولیه اطلاعات سیستم‌ها باشه.

اینطوری دل هما رو هم به دست میارم که یه زمان بهم چنین دستوری داده بود:

برداشت من از نوشته هاتون اینه علاقه ندارید این جا بحث های ریاضی بکنید، ولی یک پیشنهاد: اگه میشه با یه سرفصل مشخص این بحث های ریاضی رو بکنید. فکر کنم خیلی جذابه و در مورد خودم باعث میشه ریاضیات رو بهتر بفهمم. فکر کنم افرادی هم باشند که به این بحث ها علاقه دارن.

پیش نوشت دو (برای هما): هما جان. همون‌طور که مطمئناً به خوبی می‌تونی حدس بزنی، بخش قابل توجهی از مباحث مرتبط با سیستم‌های پیچیده در حال حاضر، از جنس شبیه سازی‌های نرم افزاری کامپیوتری هست. حالا هر کس بسته به نیاز خودش، المان‌های ساده‌ی سیستم رو تعریف می‌کنه این المان‌ها رو در تعامل با هم قرار می‌ده و رفتار سیستم رو در طول زمان مشاهده و اصلاح می‌کنه.

حالا دیگه نحوه‌ی پیاده سازی به این برمی‌گرده که هر کسی دستش برای کار با چه ابزاری بازتره. برنامه نویس‌ها قاعدتاً سراغ پلتفرم‌هایی میرن که بهشون زیرساخت‌های OOP یا Object Oriented Programming رو بده. دانشجوهای دانشگاهی معمولاً چون از صفر نمی‌تونن چنین سیستم‌هایی رو پیاده سازی کنند، سراغ ابزارهای آماده‌تر مثل MATLAB میرن.

بنابراین، کاربرد ریاضی در تحلیل سیستمهای پیچیده، بیشتر به نظارت و ارزیابی و سنجش برمی‌گرده.

چنانکه در دنیای واقعی هم، فیزیک بیشتر کار سنجش رو انجام می‌ده و بر اساس این سنجش، سعی می‌کنه تغییراتی در جهان ایجاد کنه. ما به عنوان بخشی از عالم هستی در میانه‌‌ی عالم هستی که در حال خلق هست، قرار گرفته‌ایم و مدام اندازه گیری می‌کنیم و اگر بتوانیم تصویری واقعی‌تر از جهان در آینده‌ رو به دست بیاریم خوشحال می‌شیم و نتیجه می‌گیریم که نظریه‌های علمی‌مون به درک بهتر محیط کمک کرده‌اند.

ریاضیات سیستم های پیچیده هم، بیشتر نگاهش مبتنی بر اندازه گیری و سنجش هست و البته اگر بتونه خوب اندازه گیری کنه، می‌تونه به تغییر سیستم‌ها هم اقدام کنه.

ما در فیزیک، مدتهاست که از اندازه گیری عبور کرده‌ایم و الان در حال تاثیرگذاری روی سیستم هستیم.

در ریاضیات سیستم‌های پیچیده، هنوز داریم سعی می‌کنیم اندازه گیری رو بهتر یاد بگیریم و روش‌های بهتری رو دیدن محیط خلق کنیم.

سعی می‌کنم اینجا (و اگر حال و حوصله‌ای بود بعداً در ادامه‌ی این بحث) نظریه اطلاعات رو به عنوان یکی از ابزارهای ریاضی که به درک سیستم های پیچیده کمک می‌کنه در حد خیلی ساده و ابتدایی فهم خودم، توضیح بدم.

اصل بحث- اطلاعات

چیزی که شاید هنوز به درستی نمی‌دانیم چیست

اگر درس‌های دانشگاهی مدیریتی رو بخونی، احتمالاً بلافاصله‌ی بعد از شنیدن واژه‌ی اطلاعات، مجموعه‌ای از روضه‌های آماده در زمینه‌‌ی تفاوت اطلاعات و داده‌ (Data vs. Information) خواهی داشت و بعیده که کلمه یا مفهوم اطلاعات بتونه خیلی هیجان زده‌ات بکنه.

اما اگر اون آموخته‌ها و نامگذاری‌ها رو کنار بگذاریم، مفهوم اطلاعات به صورت مستقل و مجرد، چندان قابل تعریف نیست.

تو الان داری این وبلاگ رو می‌خونی به امید اینکه چیزی به “اطلاعات” تو اضافه بشه.

همچنین خیلی وقتها می‌گیم فلانی اطلاعاتش در این زمینه خیلی زیادتر از منه.

به نظر میاد حتی اگر قادر به اندازه‌گیری اطلاعات نباشیم، اون رو قابل سنجش و قابل مقایسه می‌دونیم.

جالب اینجاست که ظاهراً اطلاعات، یا ثابت می‌مونه یا افزایش پیدا می‌کنه.

تا حالا نشنیده‌ام کسی بگه با یکی حرف زدم، اطلاعاتم خیلی کاهش پیدا کرد!

معمولاً می‌گیم: چیزی بهم اضافه نشد (احتمالاً اگر مباحث ترمودینامیک رو یادت باشه، با شنیدن چیزی که زیاد می‌شود، اما کم نمی‌شود، یاد انتروپی می‌افتی).

از طرف دیگر، اطلاعات بار ارزشی نداره. بر خلاف لغت‌هایی مثل حقیقت و واقعیت، اطلاعات مفهومی است که سوگیری ندارد:

اطلاعات مفید، اطلاعات غیرمفید، اطلاعات درست، اطلاعات نادرست، اطلاعات ارزشمند، اطلاعات دروغ

علاوه بر این توضیح من، یک چیز دیگه هم می‌دونیم که امروز، عصر اطلاعات هست.

البته نمی‌دونم اگر بهمون بگن که در مورد تفاوت عصر اطلاعات، با مثلاً عصر دانش یا عصر تکنولوژی صحبت کنیم، چقدر می‌تونیم حرفه‌ای و عمیق و علمی، توضیح بدیم.

البته گنگ بودن مفهوم اطلاعات، نباید خیلی نگرانمون کنه.

به قول دائره‌المعارف استنفورد، ما هنوز درک درستی از مفهوم انرژی هم نداریم و اون رو به شکل‌های مختلف، مفهوم پردازی کرده‌ایم: انرژی جنبشی، انرژی پتانسیل، انرژی الکتریکی، انرژی هسته‌ای و …

در ظاهر، هر کدوم اینها دارن حرف متفاوتی می‌زنن، اما در نهایت رابطه بین اینها و نحوه تبدیل شدنشون به یکدیگر رو تا حد خوبی می‌فهمیم و حتی اگر نتونیم ذات انرژی رو به خوبی توضیح بدیم، باز هم می‌تونیم اون رو به تسخیر خودمون در بیاریم و به خدمت بگیریم.

نگاه مبتنی بر “اطلاعات” می‌تواند درک عمیقی از جهان به ما بدهد

از دوران ما قبل علم که بگذریم، رایج ترین و معتبرترین مدلی که ما برای درک جهان داریم، مدل زمان و مکان و ماده و انرژی است (اینکه اینها رو چهار تا بگیریم یا سه تا یا دو تا یا یکی، تغییری در اصل ماجرا ایجاد نمی‌کنه).

لغت مدل رو عمداً به کار می‌برم. چون ما می‌دونیم که هر توضیحی صرفاً یک مدل هست و به اندازه‌ای که می‌تونه جهان اطراف ما را تحلیل و آینده‌ی ما رو پیش بینی کنه و قدرت تاثیرگذاری ما رو روی محیط افزایش میده، مورد احترام قرار می‌گیره.

اما بیا به هم به یک سناریو فکر کنیم:

در یک لحظه، هر کس که در جهان موبایل داره، اسکرین شات آخرین مکالمه‌ی تلگرامی یا پیامکی یا واتس اپی موبایل خودش رو بگیره و به صورت تصادفی برای یک نفر دیگه در دفتر تلفنش ارسال کنه.

یک ثانیه بعد، سرنوشت جهان عوض شده. حتی می‌تونیم بگیم جهان در این یک ثانیه، دچار تکینگی شده. تاریخ یه جورایی به قبل و بعد از این نقطه تقسیم خواهد شد.

رابطه‌های عاطفی در هم می‌شکنه یا ایجاد میشه. روابط سیاسی جابجا می‌شه. اقتصاد تغییر میکنه و دیگه هیچی مثل قبل نیست. نمی‌گم بهتر یا بدتر. می‌گم مثل قبل نیست.

چه اتفاقی افتاد؟ کل میزان جابجایی ماده و انرژی که از یک ثانیه قبل تا الان اتفاق افتاده چقدر بوده؟ قطعاً به نسبت روند عادی جهان، مقدار ناچیزی بوده.

اگر فرض کنیم همه متوقف شن و این کار رو انجام بدن، تقریباً از لحاظ فیزیکی میشه گفت ظاهر جهان تغییر خاصی نداشته. اما متحول شده.

اینجا هم با ارسال و دریافت پیام‌ها از طریق کابل‌های برق و امواج سر و کار داریم. اما حرف من اینه که با معیارهای سنجش در پارادایم رایج، این جابجایی خیلی زیاد نبوده (در مقایسه با جابجایی یک ناو هواپیمابر از غرب تا شرق جهان که جابجایی ماده و انرژی بیشتری ایجاد می‌کنه اما اثرش از این سناریوی فرضی من به مراتب کمتره).

ما فقط توزیع اطلاعات رو در جهان تغییر دادیم.

سناریوی من یک حالت خیلی شدید بود و به قول اهل دانشگاه، Strong Form محسوب می‌شد. اما شکل Weak Form و ضعیفش، چیزیه که همین الان در حال انجامه! استفاده‌ی دائمی ما از موبایل و وسایل ارتباطی و شبکه های اجتماعی، حجم گسترده‌ای از تحولات رو در دنیا داره ایجاد می‌کنه که اگرچه نتایجش رو می‌بینیم، اما مکانیزمش با مترهای رایج، به سادگی قابل اندازه گیری نیست.

همه صرفاٌ می‌دونیم و لمس می‌کنیم که تحولات حاصل از وضعیت فعلی، کوچک نیست. این مغز متصل جهانی، به شیوه‌ای متفاوت و پیچیده‌تر فکر می‌کنه.

در این مرحله، می‌توانیم تعدادی سوال کلی بپرسیم:

آیا با سناریوی پیشنهادی من، حجم اطلاعات موجود در کل جهان افزایش پیدا کرده یا ثابت مونده؟

آیا صرفاً اطلاعات از جایی به جای دیگه منتقل شده؟

آیا معیار و مقیاسی برای اندازه گیری این اطلاعات جابجا شده وجود داره یا قابل تصوره؟

آیا میشه به شیوه‌ی مشابهی، با گوش دادن به یک سخنرانی تلویزیونی یا رادیویی،‌ محاسبه کرد و شمرد که واقعاً چقدر اطلاعات عرضه و جابجا شده؟

آیا – در ارجاع به سرزمین موریانه‌ای مورد علاقه‌ی من – میشه اطلاعات ذخیره شده در ساختار اجتماعی موریانه‌ها رو اندازه گیری کرد و مثلاً‌ با اطلاعات ذخیره شده در ساختار اجتماعی شهر خودمون مقایسه کنیم و ببینیم که کدام، مطلع‌تر هستند؟

آیا من می‌تونم همزمان، به اعضای یک جامعه انسانی این حس رو بدم که اطلاعاتشون بیشتر از قبل شده و در عین حال، اطلاعات اون جامعه رو ازشون بگیرم و کاهش بدم؟

اصلاً اطلاعات رو میشه نابود کرد یا صرفاً میشه جابجا کرد؟

برای پیدا کردن پاسخ چنین بحث‌هایی (که البته اگر بدونیم کدوم مدل رو مورد استفاده قرار می‌دیم، پاسخ همه شون مشخص و شفاف و قابل بحث هست) لازمه که مدلی برای تعریف و سنجش اطلاعات داشته باشیم.

اون وقت می‌تونیم مثلاً‌ در مورد توزیع اطلاعات در میان سهامداران حقیقی و حقوقی بورس تهران و یا مثلاً‌ حجم کل اطلاعات مستقر شده در ساختار بورس به عنوان یک سیستم پیچیده در مقایسه با حجم اطلاعات چند سال قبلش (و احتمالاً‌ روند چند سال بعدش) اظهار نظر کنیم.

اینجا لازم هست که بحث پیام و محتوای پیام رو از هم تفکیک کنیم.

من ممکنه پیامی طولانی و حجیم برای تو ارسال کنم، اما Information Content یا محتوای اطلاعاتی اون کم باشه.

البته خود واژه‌ی پیام هم، به اندازه‌ی واژه‌ی اطلاعات، مبهم هست. در تعریف و نگاهی که من دارم، هر شیء رو می‌تونی یک پیام در نظر بگیری.

یعنی پراید سفید و قورباغه‌ی سبز و پست وبلاگ روزنوشته و پیامک موبایل، صرفاً چهار نوع پیام متفاوت محسوب می‌شن.

به اینجا که می‌رسیم، هر کس تعریف متفاوتی از محتوای پیام داره. مثلاً پوپر، به غیرمنتظره بودن اشاره می‌کنه و به شکلی دیگر (و البته مشابه) میگه: ارزش محتوای یک پیام به اندازه‌ی گزاره‌هایی هست که باهاش نقض می‌شه.

هما، به این مثال فکر کن:

فرض کن الان پشت در بسته‌ی یک اتاق نشسته‌ایم.

یک نفر میاد و می‌گه: داخل این اتاق هیچ چیزی نیست.

این پیام، قطعاً محتوا داره. یعنی می‌تونی بگی Information Content داشته.

حالا فرض کن قبلش من بهت گفته‌ام: داخل این اتاق یک گاو صندوق گذاشته‌ام. یک میز هم وسط اتاق هست. دسته چک من هم داخل اتاق هست و وقتی برویم داخل، بدهی‌هایم را به تو خواهم داد.

حالا همون آدم میاد و میگه: داخل این اتاق هیچ چیزی نیست.

الان این پیام، چند گزاره رو نقض کرد: فهمیدیم که گاوصندوق من اون تو نیست. فهمیدیم که میز در کار نیست. فهمیدیم که دسته چکی در کار نیست و فهمیدیم که وقتی داخل برویم، تو طلب‌هایت را دریافت نخواهی کرد.

با وجودی که پیام یکسان هست، محتوای اون، بر اساس سایر پیام‌هایی که در محیط هست و اینکه دریافت کننده‌ی پیام چه کسی هست، می‌تونه Information Content متفاوت داشته باشه.

این می‌تونه یه مدل برای سنجش و اندازه گیری اطلاعات باشه.

اما من مدل کلود شانون رو که پدر نظریه اطلاعات محسوب میشه، برای این بحث‌مون ترجیح می‌دم:

فرض کن ما الان یک سیستم داریم (ساده یا پیچیده مهم نیست).

این سیستم می‌تواند به صورت بالقوه، ده وضعیت (State) مختلف داشته باشه که اونها رو با S1 و S2 و S3 و …  نشون می‌دیم.

تمام این State‌ها رو اگر کنار هم قرار بدی و تمام حالات محتمل رو بدونی، می‌تونی بگی که State Space رو برای اون سیستم می‌شناسی.

همچینن فرض کن من می‌دونم که احتمال اینکه الان سیستم در هر حالت باشه چقدره.

یعنی علاوه بر S1 تا S10 ما احتمالات رو هم از P1 تا P10داریم.

حالا یه نفر میاد میگه: من می‌دونم که این سیستم، در اولین گام تغییر قراره به وضعیت S4 بره.

آیا خبر این فرد مهم هست؟ آیا اطلاعات ارزشمندی رو به ما داده؟

 فرض کن که p4 مثلاً ۹۹% باشه.

پس ما خودمون می‌تونیم حدس بزنیم که به احتمال زیاد، سیستم به وضعیت S4 میره.

اطلاعات اون آدم وقتی برای من ارزشمنده که المان سورپرایز در پیامش بیشتر باشه.

شنون، یه مدل پیشنهادی برای سنجش میزان عدم قطعیت داره که می‌تونه مفید باشه (لغت پیشنهاد خیلی مهمه):

اون پایه‌ی لگاریتم خیلی مهم نیست.

مهم روح لگاریتم هست که وقتی احتمال کوچیک میشه، به ما عدد بزرگتری میده و نشون می‌ده که اون پیام، داره اطلاعات ارزشمندتری رو حمل می‌کنه.

من پایه‌ی دو رو برای لگاریتم ترجیح می‌دم چون به فضای دیجیتال نزدیک‌تره.

پس اگر یک نفر به من بگه که شماره آخر موبایل تو ۳ هست، به من ۳٫۳۲ بیت اطلاعات مفید داده (احتمال سه بودن، یک دهم هست).

اگر بگه شماره‌ی دوم موبایل تو مثلاً ۷ هست، باز هم به من ۳٫۳۲ بیت اطلاعات مفید داده (باز هم احتمال ۷ بودن، یک دهم هست)

اگر از اول مثل بچه‌ی آدم بیاد بگه دو رقم آخر تلفن تو ۷۳ هست، به من ۶٫۶۴ بیت اطلاعات مفید داده (چون احتمالش یک صدم هست).

اینجاست که مدل پوپر (لااقل برای من) دوست داشتنی نیست. چون:

اگر طرف آزار داشته باشه و اول بیاد ۷ رو بگه برای من ۹ گزینه رو حذف کرده. بعد بیاد ۳ رو بگه، دوباره ۹ گزینه رو حذف کرده. پس ۱۸ واحد اطلاعات داده.

اما اگر آدم سالمی باشه و بیاد از اول ۷۳ رو بگه، ۹۹ واحد اطلاعات رو حذف کرده.

به نظرم اگر هدف من کلاً دونستن دو رقم آخر تلفن تو باشه، دلیل نداره محاسبات، دو جواب مختلف بده (البته می‌تونی فرض کنی که خرد کردن و تحویل تدریجی اطلاعات، ارزش اطلاعات رو کم می‌کنه که الان بحث من نیست).

اما قشنگ‌ترین کار کلود شانون پیشنهاد انتروپی اطلاعاتی یک سیستم هست:

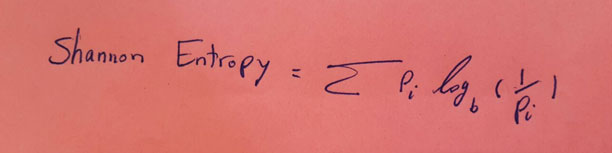یه جورایی امید ریاضی ترکیب محتوای اطلاعاتی یک سیستم رو حساب کرده.

به این مثال ساده فکر کن:

تو یه سکه داری که باهاش شیر یا خط بازی می‌کنی. احتمال اینکه سکه از رو بیفته یک دوم هست. احتمال اینکه از پشت هم بیفته یک دوم هست. و سیستم شیر یا خط کلاً دو وضعیت S1 و S2 بیشتر نداره که احتمال هر حالت هم ۰٫۵ هست:

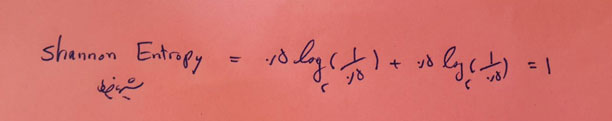چون پایه رو ۲ فرض کردم، میشه گفت: اطلاعات حاصل از انداختن یک سکه رو، در بهترین حالت و فشرده‌ترین حالت میشه در یک بیت ذخیره کرد.

ممکنه بگی!

خاک بر سرت محمدرضا! این همه ضرب و تقسیم! خوب این که از اول معلوم بود!

بذار برای اینکه کمتر فحش بخورم یه استفاده‌ی دیگه از کلود شانون بکنم:

یه کلاس کوچیک ده نفری رو در نظر بگیر که بچه‌ها به شکل U می‌شینن توش:

الان من میام به تو دقیقاً می‌گم که چه کسی کجا نشسته (هیچ کدوم هم ترجیح خاصی ندارن و هر جایی ممکنه بشینن).

ارزش این پیام من چقدره؟ تعداد کل حالت‌ها !۱۰ (ده فاکتوریل) هست و احتمال هر کدوم برابر که اگر حساب کنی میشه:

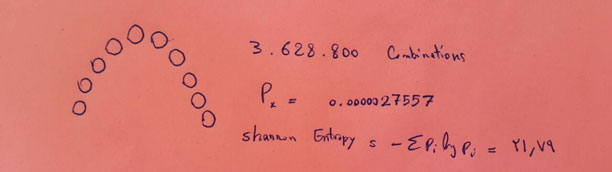احتمالاً هنوز هم خیلی از من راضی نیستی.

چون می‌گی به جای این همه کار پیچیده، کافی بود که فکر کنی عدد !۱۰ در مبنای دو چند بیتی می‌شه.

اما یادت نره که الان همه‌ی احتمالات برابر هستند و به محض اینکه احتمالات برابر نباشن، دیگه چاره‌ای جز توسل به انتروپی شنون نداریم.

می‌تونی اگر وقت داشتی به این سوال فکر کنی: یه نفر میاد میگه: فهمیده‌ام که علی و مریم این هفته با هم دوست شده‌اند و حتماً در کلاس کنار هم می‌نشینند.

سوال من اینه که این خبر خاله زنکی، چند بیت می‌ارزه؟ (حساب کنی فکر کنم حدود ۲٫۳ بیت ارزش داره!)

حالا میشه بهتر فهمید که یکی از کاربردهای شبکه های اجتماعی به عنوان یک سیستم پیچیده چیه.

ما با هر بار لایک زدن یا نزدن یا فالو کردن یا نکردن، داریم اطلاعات “تولید” می‌کنیم و از سوی دیگه، انتروپی اطلاعاتی جامعه رو کاهش می‌دیم.

چیزی که ذی‌نفعان زیادی داره و خیلی‌ها حاضرن براش پول بدن و ظاهراً همین کار رو هم کرده‌اند. چون ما داریم مجانی از این سیستم‌ها استفاده می‌کنیم!

وقتی یک سیستم پیچیده رو شبیه سازی می‌کنیم، در هر لحظه، می‌تونیم از روی تمام سناریوهای احتمالی، برآورد کنیم که انتروپی اطلاعاتی سیستم چقدر تغییر می‌کنه.

همین مسئله رو در مورد تمام جهان هم میشه مطرح کرد که الان خارج از این بحث میشه.

پی نوشت یک: بحث Big Data یکی از دانش‌ها و روش‌هایی هست که ما برای درک بهتر سیستم‌های پیچیده به کار می‌گیریم.

اما آشنایی سطحی با Big Data در شرکتها و سازمان‌ها و کسب و کارها، صرفاً باعث شده که حجم بسیار زیادی از اطلاعات ذخیره و نگهداری بشه. در واقع هر چیزی که در یک سیستم، دیده‌ایم و توانسته‌ایم ثبت کنیم، ثبت کرده‌ایم.

بحث محتوای اطلاعاتی یا Information Content در کنار بحث Big Data می‌تونه کمک بزرگی برای تشخیص پاسخ این سوال کلیدی باشه که: چه اطلاعاتی را نباید ذخیره کنیم؟ و یا به عبارت دیگر، آیا هزینه ذخیره کردن یک مجموعه داده‌ی خاص، با توجه به فایده‌هاش توجیه پذیر هست یا نه.

پی نوشت دو: مقاله A mathematical theory of communication تقریباً نطفه‌ی تولد فرم کلاسیک نظریه اطلاعات محسوب می‌شه.

پی نوشت سه: یه سر زدم ویکی پدیا. دیدم یک مطلب خیلی خنده دار در مورد نظریه اطلاعات نوشته شده با یه زبانی که بعیده کسی راحت بفهمه (شرح نظریه اطلاعات در ویکی پدیا) نویسنده‌ی متعصب اون مطلب، انقدر نگران استفاده از کلمه‌ی عربی اطلاعات بوده و سعی کرده همه چی رو فارسی بکنه که بعیده یه فارسی زبان، دیگه بتونه بفهمه مطلب رو.

چقدر جالبه که راجع به نظریه‌ای کار کنی که تفاوتی بین سنگ و سگ نمی‌بینه (جز در حجم اطلاعاتی که در ساختارشون ذخیره شده) و انقدر باهاش بیگانه باشی که هنوز پای تو در تعصبات کور قومی و کلامی گیر باشه.

آموزش مدیریت کسب و کار (MBA) دوره های توسعه فردی ۶۰ نکته در مذاکره (صوتی) برندسازی شخصی (صوتی) تفکر سیستمی (صوتی) آشنایی با پیتر دراکر (صوتی) مدیریت توجه (صوتی) حرفه ای گری (صوتی) هدف گذاری (صوتی) راهنمای کتابخوانی (صوتی) آداب معاشرت (صوتی) کتاب «از کتاب» محمدرضا شعبانعلی کتاب های روانشناسی کتاب های مدیریت